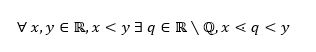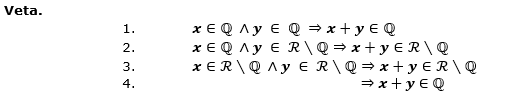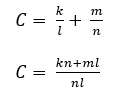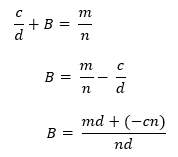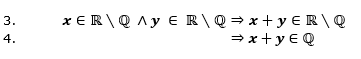Matematika

Iacobus Po 2 august 2021 - 15:49

Dobrý deň prajem.

Myslím, že som to spomínal, objavil som znovu čaro matematiky. Viete, matematiku som mal vždy rád. Vypočítať príklad pre mňa predstavuje určite vzrušenie. Keď to píšem, môže to vyznieť komicky. Prečo je to tak? Nazdávam sa, že je to celkom zrejmé. Počítať priklad znamená riešiť problém. Vypočítaný príklad preto znamená vyriešený problém. Ja si teda myslím, že každý má rád vyriešené problémy, každého to uspokojuje. Matematické probemy nebudú tak výnimkou.

Na matematike ma fascinuje, že veľakrát opisujeme obstraktný pojem. Préve toto mnohých odrádza, myslia si, že je to zbytočné. Avšak nie je, tieto matematicke opisy sa vyskytujú vo fyzike, takže celý svet okolo nás je matematika.

Matematika sa zdá pre niekoho zložitá, ja hovorím, že je dômyselná a elegantná.

Teraz mám chuť každému hovoriť o tom, čo som práve v matematike objavil. Lenže nestretávam sa s pochopením. Moji známi nechcú riešiť matematku. No, preto mám fórum, aby som napísal, čo chcem. Takže budem teraz vás zaťažovať matematikou. Pričom je zrejmé, koho to nezaujíma, tak si to neprečíta. A možno sa najde niekto, kto bude ochotný so mnou diskutovať.

Pozdravujem.

Iacobus Po 2 august 2021 - 16:56

Na začiatok som si pripravil jednoduchú vec z diskrétnej matematiky. Budem hovoriť o "klasickej" logike.

Poviem dve vety a tretia z nich bude logicky vyplývať:

Ak prší, cesta je mokrá.
Prší.

Z čoho logicky odvodíme, že:

Cesta je mokrá.

Myslím si, že predchádzajúci úsudok je zrejmý pre každého. Teraz poviem druhú dvojicu viet:

Ak prší, cesta je mokrá.
Ak prší, cesta nie je mokrá.

Čo vieme usúdiť? Je cesta mokrá alebo nie je mokrá? Toto už nie je až také zrejmé. Keď chceme zistiť, čo z toho usúdime, musíme sa pozrieŤ bližšie na pravdivostné hodnoty logických spojok.

Výrok je oznamovacia veta (tvrdenie), o ktorej môžeme jednoznačne rozhodnúť, či je buď pravdivá, alebo nepravdivá.
Vágne vety, ako "život je pekný", nepovažujeme za výroky, lebo je to vecou názoru. Z uvedeného je zrejmé, že opytovacie, či rozkazovacie vety nie sú výrokmi. V našom prípade sú výroky: "prší" a "cesta je mokrá".

Pravdivostnú hodnotu výroku v klasickej logike označujeme ako:

pravdivý, (označí sa 1) a
nepravdivý, (označí sa 0).

(Okrem toho existuje aj fuzzy logika, ktorá priraďuje hodnoty pravdivosti v intervale 0 až 1. Tým sa nebudeme zaoberať.)

Jednoduché výroky môžeme spájať do zložitejších pomocou logických spojok:

konjunkcia výrokov. Čítame "a zároveň" alebo len "a". Označujeme "∧".
disjunkcia výrokov. Čítame "alebo". (Táto spojka nemá vylučovací charakter). Označujeme "∨".
implikácia výrokov. Čítame "Ak..., tak (potom)..." Označujeme "⇒".
ekvivalencia výrokov. Čítame "...práve vtedy, keď..." Označujeme "⇔".

Pravdivosť zložených výrokov záleží od pravdivosti jednoduchých výrokov takto:

A	B	A∧B	A∨B	A⇒B	A⇔B
1	1	1	1	1	1
1	0	0	1	0	0
0	1	0	1	1	0
0	0	0	0	1	1

Teraz už môžeme konečne riešiť náš problém. Zložený výrok: "Ak je pravda, že ak prší, cesta je mokrá a zároveň prší, tak potom cesta je mokrá." Zapíšem ako zložený výrok: ((A⇒B)∧A)⇒B, pričom A = prší. B = cesta je mokrá.

Teraz si vyriešime všetky situácie, ktoré môžu nastať a z toho usúdeme, či máme pravdu v tom, čo sme si mysleli.

A	B	A⇒B	(A⇒B)∧A	((A⇒B)∧A)⇒B
1	1	1	1	1
1	0	0	0	1
0	1	1	0	1
0	0	1	0	1

Z toho vyplýva, že nech je A a B pravdivé alebo nepravdíve, zložený výrok je vždy pravdivý. Takže mali sme pravdu,v tom čo sme hovorili o prvých dvoch vetách. Náš úsudok bol správny. Teraz riešme druhé dve vety: Ak prší, cesta je mokrá. Ak prší, cesta nie je mokrá.

Mysleli sme si, že tie dve vety hovoria niečo o ceste? Vôbec nie, ony hovoria o počasí, teda, že vôbec neprší. Pozrime sa na to pomocou pravdivostných hodnôt tých výrokov. (Pozn. non-A znamená negácia výroku, teda opačné pravdivostné hodnoty.

A	B	non-A	non-B	A⇒B	A⇒non-B	(A⇒B)∧(A⇒non-B)	((A⇒B)∧(A⇒non-B))⇒non-A
1	1	0	0	1	0	0	1
1	0	0	1	0	1	0	1
0	1	1	0	1	1	1	1
0	0	1	1	1	1	1	1

Teda znova sme ukázali, že nech sú pravdivostné hodnoty jednoduchých výrokov akékoľvek, vždy dostaneme pravdivý výrok, takže z dvoch viet: Ak prší, cesta je mokrá. Ak prší, cesta je suchá. Vyplýva: Neprší.

Táto výroková formula sa nazýva reductio ad absurdum a používa sa pri matematickom dôkaze sporom.

Iacobus Ut 3 august 2021 - 9:25

Neviem, do akej miery vás zaujalo to, čo som písal o výrokoch. Za seba by som povedal, že som očarený.

Keď som však svoje nadšenie zdieľal s rodinou, tak ma až vysmiali. Zdalo sa im to úplne mimo realitu. A je to vtipná situácia, keď si predstavíte človeka, ktorý to horlivo vysvetľuje, a druhého, ktorý vôbec neprijíma, čo hovoríte. Vždy, keď prší, tak si v mysli oživujem tú vtipnú predstavu.

No späť k veci. Ukázal som vám jeden prípad, kedy je zložený výrok pravdivý za každých okolností. Volá sa to tautológia, pričom existuje viacero takých výrokov, ktoré môžeme nazvať tautológia, to som zabudol napísať. A má to význam v matematických dôkazoch, ako som spomenul. Nejakým opakom by mohla byť kontradikcia, ktorá je vždy nepravdivá.

Dôkazy v matematike

Na matematike je krásne aj to, že existuje iba niekoľko základných axióm a všetko ostatné sa z nich odvodzuje pomocou dôkazov. Dobrý správa pre vás. Matematiku sa nemusíte učiť naspamäť, matematiku si odvodzujete. Tých typov dôkazov je niekoľko. Nemá zmysel, aby som uvádzal všetky príklady. Napíšem asi len jeden dôkaz, lebo ten by som chcel použiť neskôr pri inom dôkaze.

V matematike musíme myslieť kriticky a všetko možné spochybňovať.

Veta. Druhá odmocnina z 2 je iracionálne číslo.

(Pozn.: Iracionálne čísla sú také, ktoré nevieme napísať ako pomer celých čísel Z/N, pričom N je rôzne od nuly.)

Veríte mi vetu, ktorú som povedal? Nemali by ste. Tak číslo dáte do kalkulačky a zdá sa, že desatinný rozvoj nemá konca. Tak usúdite, že je iracionálne. Stačí to v matematike ako dôkaz? Povedzme, že vaša kalkulačka počíta na 50 desatinných miest. Čo ak na 51. mieste sa rozvoj končí? Potom by odmocnina z 2 bola racionálna. Je zrejmé, že toto ako spoľahlivý dôkaz nepovažujeme.

Poďme si to dokázať. Budem dokazovať sporom, takže dokážem, že negácia pôvodného výroku je zjavná nepravda.

Dôkaz. Druhá odmocnina z 2 je racionálne číslo. No, nech by aj bola, tak potom ho viem napísať ako pomer dvoch nesúdeliteľných prirodzených čísel Z,N.

Takže platí:

Teda Z číslo je párne, lebo je dvojnásobok N. Ak Z² je párne, tak aj Z je párne. Otázka znie, či naozaj. Ak vieme, že párne číslo je deliteľné dvomi, tak pre celé čísla platí, že sa dajú napísať ako 2 krát n. Potom (2n)² = 4n². Teda druhá mocnina párneho čísla je párna, (okrem toho je aj deliteľná štvorkou.) Ak viem napísať, že nepárne číslo je 2n+1. Tak potom jeho druhá mocnina je (2n+1)² = 4n² + 4n + 1 = 4(n² + n) + 1. Teda je nepárna. Môžem povedať, že ak mám nepárne číslo, tak jeho štvorec nikdy nie je párny. Obmena implikácia je, že ak mám párny štvorec, tak mám párne číslo. (Obmena implikácie je metódou nepriameho dôkazu. Zapisujeme: A⇒B = non-B⇒non-A).

Vrátime sa k odmocnine. Teraz vieme, že Z je párne, môžem ho teda napísať ako Z = 2n. Substituujem do pôvodnej rovnice a dostanem:

2 N² = (2n)²

2 N² = 4 n²

N² = 2 n²

Odtiaľ vyplýva, že N² je párne, lebo je to dvojnásobok n². Už máme dokázané, že ak N² je párne, tak aj samo N je párne.

V našom predpoklade sme požadovali, aby N/Z boli nesúdeliteľné, lenže to nie je pravda, keďže obe sú párne, tak sú určite deliteľné 2. To je spor k nášmu výroku, preto platí výrok, že druhá odmocnina z 2 je iracionálna.

Čo sme vlastne dokázali? Len to, že dané číslo neviem napísať ako pomer Z/N, takže to nie je racionálne číslo. Správna otázka teraz znie, existuje vôbec odmocnina z 2?

Iacobus St 4 august 2021 - 14:32

Včera, keď som písal o druhej odmocnine z 2, som zabudol napísať takú perličku s tým súvisiacu, vďaka ktorej si ten dôkaz lepšie zapamätáte.

Pytagorejci

Pytagoras zo Samu žil v 6. storočí pred n. l. V rodnom meste Samos nemal priestor na šírenie svojich myšlienok, a tak sa presťahoval do Krotónu v dnešnom Taliansku. Našiel si tam prívržencov, ktorí ho uznávali. Ľudia združení okolo Pytagora sa nazývali pytagorejci, bol to vlastne spolok alebo skôr sekta, pretože mali prísne pravidlá, ktoré museli dodržiavať. Zaujímavé je, že ich symbolom bol pentagram, zrejme kvôli faktu, že pomer strany a uhlopriečky v pravidelnom päťuholníku je zlatý rez. Pentagram pre nich znamenal prosperitu.

Keď som hľadal Pytagorovu podobizeň, našiel som toto:

Pekný obrázok. Určite si nikto nemyslí, že Pytagoras tokto v skutočnosti vyzeral. Je to len kresba a určite nie je taká stará ako Pytagoras. Stačí nakresliť stršieho bradatého pána s múdrym výrazom a Pytagoras je na svete. Rovnako tak by však mohol vyzerať Archimedes, Táles, Euklides a pod.

Toľko úvod o Pytagorovi, teraz sa pozrime na racionálne a iracionálne čísla.

O existencii racionálnych čísle vedeli už aj pytagorejci v antickom Grécku. Teraz nebudem zrejme celkom férový. Pytagorejci boli podľa mňa práve tým prototypom matematikov, o ktorých si aj dnes ľudia myslia svoje. Pod slovom "svoje" mám na mysli, že je to uzavretá skupina prinajmenšom čudných ľudí, žijúcich vo svojom svete, kde riešia veci, ktoré sú zdanlivo zbytočné. Inými slovami o bežných veciach s nimi nie je žiadna reč. Ba dokonca oni sú úplne mimo realitu.

Pytagorejci si riešili matematicke problémy. Významný je poznatok o po Pytagorovi nazvanej vete, ktorú ale poznali už pred ním starí Egypťania a zrejme aj iné národy. Zaujímavý ich poznatok je, že súčet uhlov v každom trojuholníku je dvakrát pravý uhol. Prispeli aj v poznatkoch o konštrukcii rovinných útvarov a telies. Vyznávali filozofický názor, že svet je opísateľný pomocou matematiky. Musím povedať, že všetko sú to zaujímavé veci, na ich dobu určite pokrokové.

Pytagorejci mali takmer úplne dokonalú teóriu, v ktorej vystupovali len prirodzené a racionálne čísla, ktoré sa dali zapísať ako pomer dvoch prirozených. (Dnes vieme, že je to pomer dvoch celých číseel, ktoré sú rôzne od nuly.) Mám však za to, že pytagorejci nepoznali záporné čísla, tie sa v Grécku vyskytli až v 3. storočí n. l. Nulu nechceli používať. Hovorili: "Ako može nič byť niečím?"

Pytagorejci sa hrali s úsečkami, mysleli si, že všetky čísla vedia narysovať ako dĺžku úsečky. Teda celkom logicky verili v existenciu len takćh čísel ako 1; 5; jedna polovica; tri osminy a pod. Vôbec nepočítali s tým, že môžu existovať čísla, ktoré nemajú ukončený desatinný rozvoj. V takom peknom svete žili, až kým neprišiel Hippasos z Metapontu. On narysoval štvorec s dĺžkou strany 1 a jeho uhlopriečku, ktorá mala dĺžku √2. Zapísal to nejako inak. Znak √ ešte nepoznal.

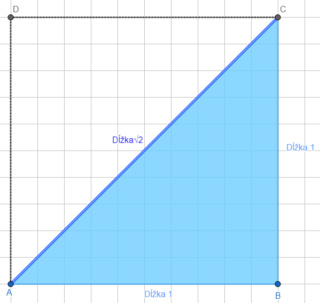
Tento rysovací počin roka by pytagorejci zrejme ešte predýchali. Lenže Hippasos ukázal, že √2 nie je pomer prirodzených čísel, nie je teda racionálne. Pytagorejcom sa v tom okamihu zrútila teória, preto vraj Hippasa utopili. Jednoducho ho podľa legendy zhodili z lode do mora. Celkom pochopiteľné. Viete si predstaviť, akí boli rozrušení? To im nemôžeme mať za zlé.

Už určite chápete, prečo som v úvode pytagorejcov označil za čudných. Ale to bola doba, zabíjalo sa kvôli matematike...

Iacobus Št 5 august 2021 - 9:41

Spomínal som dôkaz sporom v matematike. Pravdepodobne prvé príklady tejto metódy, nazývanej reductio ad absurdum, pochádzajú od gréckeho filofoza Zenóna z Eley.

Číselná os

Zenón z Eley žil v 5. storočí pred n. l. Bol predstaviteľom filozofického smeru, známeho pod názvom eleátska škola. (Opäť podobizeň, snáď nikto nečaká, že takto v skutočnosti vyzeral.)

Ovplyvnil ho Parmenides názorom, že vníma nie reality je chybné. Tu sa pohybujem na tenkom ľade, lebo o filozofii neviem veľa. Nazdávam sa, že Zenón pod vplyvom toho prišiel s niekoľkými paradoxnými úvahami – apóriami. Najznámejšou je asi tá s vystreleným šípom. Šíp nikdy nedoletí do svojho cieľa, lebo musí najskôr prejsť polovicu svojej dráhy, potom polovicu z ostávajúcej dráhy a tak ďalej do nekonečna. Podľa mňa vôbec Zenón nehovoril o reálnom šípe. O čom teda?

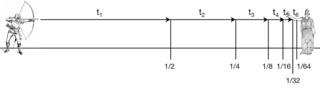
Predstavme si číselnú os. Čísla sú tam ako korálky na šnúrke. Taká predstava je vhodná pre prvý stupeň základnej školy.

Ukážem, že skutočnosť je iná. Ukážem, že medzi každými dvoma reálnymi číslami leží jedno racionálne. Zapísané matematicky: (V nasledujúcom príspevku, lebo viac obrázkov neviem vložiť.)

Iacobus Št 5 august 2021 - 9:44

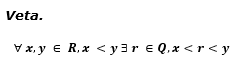
Majme číselnú os a bod x, y také, že vzdialenosť medzi nimi je väčšia ako 1 (y – x > 1). Potom medzi x, y určite leží aspoň jedno celé číslo Z.

Čo ale v prípade, keď vzdialenosť x, y je menšia ako 1? Tu potrebujem ukázať, že pre každé reálne číslo x viem nájsť aspoň jedno prirodzené číslo n také, že platí 1/n < x. Matematicky:

Čo je zjavná nepravda, takže platí to prvé.

Poďme späť k osi a bodom x, y. Vzdialenosť je menšia ako 1. Ale stále požadujem, aby y – x > 0. Aj keď je ich rozdiel veľmi malý, je to kladné reálne číslo, takže viem nájsť číslo 1/n, ktoré je od neho ešte menšie. Potom môžem napísať y – x > 1/n.

V tomto okamihu vynásobím nerovnicu n. Stane sa to, že sa na číselnej osi posuniem tak, že vzdialenosť x, y bude väčšia ako 1. To znamená, že som si chytil jedno celé číslo z. Teraz vydelím nerovnicu n. Tým sa vrátim na číselnej osi do pôvodných bodov, len z uloveného čísla z sa stane z/n. Pomer z/n je racionálne číslo, takže som dokázal, čo som chcel.

nx < z < nx

x < z/n < y

Týmto som ukázal, že medzi každými dvoma reálnymi číslami je aspoň jedno racionálne. Potom medzi tým a tým je tiež jedno racionálne a tak ďalej. Takže na každom malom úseku môžeme nájsť nekonečne veľa čísel.

O číselnej osi podľa mňa hovoril Zenón a o tom, že má nekonečne veľa čísel, preto nikdy nemáme koniec.

Iacobus Ne 8 august 2021 - 19:23

Naposledy som dokázal, že medzi dvomi reálnymi číslami, existuje aspoň jedno racionálne. Tá skutočnosť bola celkom intuitívna, ale ako som spomínal na začiatku, aj zdanlivo celkom zrejmé veci sa musia dokázať.

Os reálnych čísel – 2. časť

Teraz by som ostal v rovnakej téme a pozrel by som sa, či medzi dvomi reálnymi číslami existuje aspoň jedno iracionálne číslo. Matematicky zapísané:

Pozn. Symbol medzi R a Q (otočená lomená čiara) znamená odčítanie množín. Takže ide o množinu vzniknutú odčítaním racionálnych čísel od reálnych, teda množinu iracionálnych čísel.

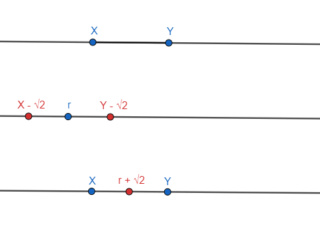
Samotná myšlienka dôkazu je podobná s myšlienkou predchádzajúceho dôkazu. Reálne čísla môžu byť veľmi blízko seba, ale chcem, aby x bolo menšie ako y. Ak to platí, tak potom od obidvoch čísel odčítam √2. Využijem skutočnosť, že medzi dvomi reálnymi číslami x, y leží určite aspoň jedno racionálne číslo r. Takže moja nerovnica bude mať tvar:

x - √2 < r < y - √2

Teraz pripočítam √2, čím získam:

x < r + √2 < y

To znamená, že medzi dvoma reálnymi číslami leží nejaké číslo r + √2. Ja by som veľmi rád to číslo prehlásil za iracionálne, aby som mal hneď hotový dôkaz, avšak to nemôžem.

V prvom rade by ste si mali klásť otázku, či je iracionálne číslo √2. Už som dokazoval, že také číslo neviem napísať ako pomer dvoch celých čísel rôznych od nuly, teda nie je racionálne. Logicky sa nám zdá, že ak nie je racionálne, tak bude iracionálne. Úvaha je dobrá, len ja zatiaľ neviem, či vôbec √2 existuje. To v tomto momente nebudem dokazovať, musíte mi veriť, že √2 existuje.

Otázka teraz znie, mám racionálne číslo r a pripočítal som k nemu √2, aké číslo dostanem. Racionálne alebo iracionálne?

Iacobus Ut 10 august 2021 - 13:19

Predchádzajúci dôkaz spočíval v tom, že som ukázal, že medzi dvomi reálnymi číslami x, y existuje aspoň jedno číslo r + √2. Veta dôkazu hovorila, že budem dokazovať iracionalitu čísla r + √2. Podľa mňa tušíte, že to číslo bude iracionálne, lenže nemáme to ešte potvrdené dôkazom.

Súčet racionálneho a iracionálneho čísla

Tak sa pozrime na súčty racionálnych čísel a iracionálnych. Na začiatok uvediem, že súčet dvoch racionálnych čísel je racionálne číslo (veta 1.). Súčet racionálneho a iracionálneho by malo byť iracionálne číslo (veta 2.). A v poslednom rade budem dokazovať súčet dvoch iracionálnych čísel (veta 3. a 4.).

Dôkaz.

Majme racionálne číslo A a racionálne číslo B. Potom A = k/l a B =m/n, pričom k, l, m, n sú celé čísla a l, n sú rôzne od nuly. Súčet C = A + B.

Takže:

Keďže kn + ml je celé číslo, aj nl je celé číslo, tak potom C je racionálne číslo. Dokázal som, čo som chcel.

Dôkaz.

2. Dokážem sporom. Povedzme, že súčet racionálneho A a iracionálneho B je racionálny D. Potom A = c/d, D= m/n, A + B = D.

Číslo B je teda racionálne, ale to je v rozpore s predpokladom, že B malo byť iracionálne. Preto je to spor, a teda platí pôvodná veta, že súčet racionálneho a iracionálneho čísla je číslo iracionálne.

To je presne to, čo sme chceli dokázať a síce, že ak mám na číselnej osi číslo r + √2, tak je celkom iste iracionálne.

Aby som to zhrnul, tak je pravda, že medzi akýmikoľvek dvomi reálnymi číslami leží aspoň jedno racionálne a zároveň aspoň jedno iracionálne číslo.

Iacobus Št 12 august 2021 - 15:25

Minulý príspevok pojednával o súčte dvoch racionálnych čísel a súčte racionálneho s iracionálnym číslom. Myslím, že intuícia nás všetkých hovorila pravdu. Dokázali sme, čo sme si mysleli. Ešte nám ostáva pozrieť sa na súčet iracionálneho a iracionálneho.

Súčet dvoch iracionálnych čísel

Veta 3. z predchádzajúceho príspevku hovorí, že súčet by mal byť iracionálny, a veta 4., že je racionálny:

Tretiu vetu neviem dokázať priamo. Ale viem ukázať, že nie je pravdivá tým, že nájdem číslo, pre ktoré tá veta neplatí.

Tak sa pozrime na súčet (√2) a (-√2). Je to nula a nula je racionálne číslo. (Stále používam √2. Vyzerá to, že iné iracionálne číslo nepoznám. A je to v podstate pravda, iné iracionálne čísla som zatiaľ neukázal, ale čoskoro ukážem.)

Tretia veta je nepravdivá, takže platí štvrtá veta, že súčet dvoch iracionálnych čísel je racionálne číslo.

Súhlasí to s našou intuíciou? Asi áno. Keď neplatí jedno, platí druhé. Lenže máme problém, pretože viem nájsť dve iracionálne čísla, ktorých súčet bude iracionálny. Napr. √2 + √2 = 2√2.

Násobenie racionálneho čísla (2) a iracionálneho (√2) je vždy iracionálne číslo. Nebudem to dokazovať. Myšlienka dôkazu je presne rovnaká, ako keď som ukazoval súčet racionálneho a iracionálneho čísla, že je iracionálny (Veta 2.). Môžete si to vyskúšať dokázať.

To znamená, že neplatí ani štvrtá veta. Klasická logika hovorí: „Tertium non datur.“ Niet tretej možnosti. Tak neplatí 3. veta, neplatí 4. veta. Čo vlastne teraz platí?

Iacobus So 14 august 2021 - 11:30

Minulý príspevok som zakončil latinskými slovami: „Tertium non datur.“ Niet tretej možnosti, odvolávajúc sa na to, že neplatí pôvodný výrok a neplatí ani jeho negácia. Klasická logika hovorí pravdu, ak hovorí, že tretia možnosť nie je. Ak tomu veríme (mali by sme), tak som urobil chybu zrejme v negácii výroku.

Negácia výrokov

Mám výrok: Prší. Negácia toho výroku znie: Neprší. Alebo aj: Nie je pravda, že prší. V každej situácii platí buď jedno, alebo druhé. Tretia možnosť, napr. že prší spolovice neexistuje.

Takže mám vety:
x, y sú iracionálne, ich súčet je iracionálny.
x, y sú iracionálne, ich súčet je racionálny.

Zdá sa nám, že jeden výrok je pôvodný, a ten druhý akoby vznikol iba negáciou pôvodného výroku. Preto platí buď jeden, alebo druhý. Lenže našiel som také číslo, že dokazuje nepravdu jedného výroku, a iné číslo, ktoré dokazuje nepravdu druhého výroku.

Už som spomenul, že bude problém v negácii výroku. Znamená to, že druhý výrok nie je negáciou prvého výroku. Len sa nám zdá, že by malo ísť o negáciu.

Ad 1. Ide o kvantifikátory. Používa sa všeobecný, ktorý znamená, že vlastnosť platí pre všetky prvky množiny. A existenčný, ktorý znamená, že vlastnosť platí pre aspoň jeden prvok množiny.

Do viet (1. – 4.) som zámerne nenapísal všeobecný kvantifikátor. Iba som zapísal, že x, y máju takú vlastnosť a to pre ne platí. Pričom je zrejmé, že tým x, y nemyslím len jedno nejaké konkrétne x, y, ale že to platí vždy pre akékoľvek x, y. Takže vety mali vyzerať formálne správne takto:

Ako negujeme výroky s kvantifikátormi? Je to jednoduché len uvediem príklad. Mám vrece jabĺk. Poviem: Všetky moje jablká sú červené. Kedy táto veta bude nepravdivá? Keď všetky jablká budú zelené? Nie. Mne stačí nájsť aspoň jedno jablko, ktoré nie je červené, a už vtedy môžem povedať, že pôvodná veta bola nepravdivá.

Naopak, poviem: Z mojich jabĺk je aspoň jedno zelené. Chcem dokázať nepravdu. Tak musím prehľadať celé vrece, a keď všetky budú iné ako zelené, tak to mám dokázané.

Čiže všeobecne v negácii výrokov s kvantifikátormi musím zmeniť kvantifikátor a povedať negáciu samotnej vlastnosti.

Takže negácia 3. vety nie je štvrtá, ale niečo ako: Existuje aspoň jedna dvojica iracionálnych čísel, ktorých súčet nie je iracionálny.
Negácia štvrtej vety by teda znela: Existuje aspoň jedna dvojica iracionálnych čísel, ktorých súčet nie je racionálny.

Ad 2. Ešte by som podotkol jednu vec. Tie moje slovné vety sú veľmi neformálne. V matematickom zápise pôvodných viet vidíme implikáciu. Mal by som ich teda prečítať takto: Pre každé reálne číslo x, y platí, že ak x je iracionálne a zároveň y je iracionálne, tak potom súčet x, y je iracionálne číslo. Pokúsim sa to znegovať, takže začnem zmenou kvantifikátora na existenčný: Existuje aspoň jedno reálne x a aspoň jedno reálne y, ... teraz by mala nasledovať negácia samotnej vety. Malý problém je v tom, že výrok nie je jednoduchý, ale zložený z dvoch výrokov implikáciou. Čo znamená nájsť negáciu? No, nájsť výrok buď jednoduchý, alebo zložený, ktorý by mal presne opačné pravdivostné hodnoty. Môžete si vyskúšať nájsť taký výrok, ja to tu nebudem predvádzať, len napíšem, že pre výrok A ⇒ B je negácia A ∧ non-B. V našom prípade: Existuje aspoň jedno reálne x a aspoň jedno reálne y také, že x, y sú iracionálne a zároveň ich súčet nie je iracionálne číslo.

Matematicky by som to zapísal takto:

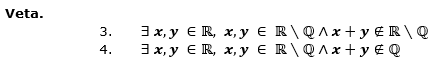
Z tohto celého opísaného vyplýva len toľko, že súčet dvoch iracionálnych čísel môže byť racionálne alebo aj iracionálne číslo. Inými slovami neviem povedať všeobecne o iracionálnych číslach, aký bude ich súčet.

Iacobus Po 16 august 2021 - 21:33

Predchádzajícim príspevkom som uzavrel strastiplnú cestu okolo číselnej osi Teraz by som sa zastavil na chvíľu pri populárnej téme, ktorá vzrušovala umelcov od renesancie snáď až dodnes. Je okolo toho dosť veľký ošiaľ a v podstate je to téma matematická. Ten súvis s prírodou a umením ponechám na vás, nakoľko vás to opantá. Iste už tušíte, že reč bude o zlatom reze.

Zlatý rez

Na začiatok by som spomenul, že zlatý podiel sa mi zdá vhodnejším menom pre zlatý rez, lebo nič sa nebude rezať, stále budeme hovoriť len o nejakých podieloch, pomeroch. Ale na Slovensku máme zaužívaný pojem zlatý rez. Naopak v angličtine je to, myslím, skôr podiel, v latinčine božská proporcia.

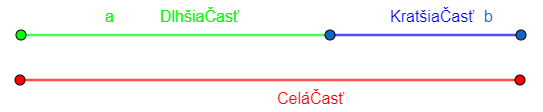
Prvá známa definícia zlatého rezu (v tom čase ho pod tým názvom nepoznali) je už v Euklidových základoch, kniha mimoriadne dôležitá pre geometriu, používaná ako učebnica do 19. storočia pochádza z 3. storočia pred n. l. Definícia znie nejako podobne: Majme úsečku, ktorú chcem rozdeliť bodom na dve časti tak, aby pomer celej úsečky k dlhšej časti bol rovnaký ako pomer dlhšej časti ku kratšej časti úsečky a ten pomer nazvem φ.

Skúsme vypočítať číselne ten pomer. Len zapíšem ako podiel slovnú definíciu, nahradím neznámymi a budem upravovať:

A je to krásny tvar kvadratickej rovnice, ktorej korene sa počítajú diskriminantom. O diskriminante som zatiaľ nehovoril, iste si ho pamätáte zo školy, preto to nebudem viac riešiť, len vypočítam a poviem, že je to akýsi vzorec na vypočítanie koreňov takýchto rovníc, pričom považujem za tragédiu, ak študent na strednej škole počíta tým ohromným vzorcom aj jednoduché príklady, napr. x² = 9. Myslíte si, ach kdeže, kto by to tak robil. Ale stáva sa to. No, korene uvedenej rovnice sú: φ1 = 1,6180... φ2 = - 0,6180... Nakoľko hovoríme o pomere strán, φ bude celkom iste len kladné.

Ste z toho ohúrení? Ja zatiaľ nie. Osobne som čakal viac. Možno vzrušenie príde v druhom príspevku o zlatom reze.

Iacobus St 18 august 2021 - 22:10

Zlatý rez - 2. časť

Spomínal som prvú definíciu zlatého rezu v Euklidových základoch, Euklides to ukáže a akosi prejde mlčaním. Vie ten pomer narysovať pomocou trojuholníka a dokáže hodnotu φ (Musíme si uvedomiť, že je to pre neho podstatne ťažšia úloha ako dnes pre nás, keďže Euklides nepoznal písmenká). Ja to spravím rovnako, iba ukážem obrázok a prejdem ho mlčaním. Nech sa páči:

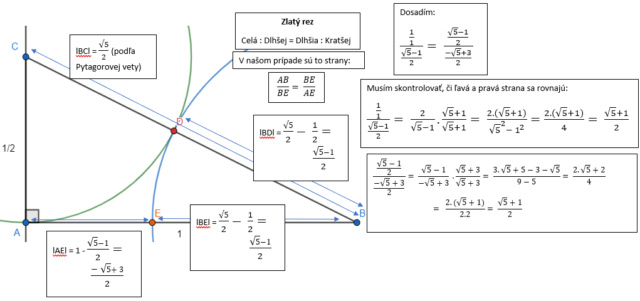
Ešte pred samotnou definíciou v Eklidových základoch, bol zlatý pomer známy v geometrii - strana pravidelného päťuholníka a jeho uhlopriečka sú v pomere 1:φ. Pytagorejci používali taký päťuholník ako tajný symbol, čudujsasvete, príde Hippasus a ukáže, že φ je iracionálne číslo. A vy už viete, ako príbeh končí. Áno, presne utopením Hippasa. Zdá sa vám, že ste už niečo také počuli? Áno, písal som, ale naozaj len niečo podobné. Tento druhý príbeh zrejme len dokazuje, že ide o legendu, pretože nie sú známe presné okolnosti, za ktorých by k údajnému utopeniu došlo. Raz je to odmocnina z 2 a raz φ. A či vôbec bol utopený, asi sa už nedozvieme.
Prečo je strana a uhlopriečka pravidelného päťuholníka v zlatom reze? Je to náhoda, alebo to vyplýva z definície? Prehliadnime si bližšie pravidelný päťuholník.

Pravidelný päťuholník je vpísaný do kružnice. Keďže päťuholník je pravidelný (čo spomínam už asi piaty raz, držím sa hesla: repetitio est mater studiorum), tak sa skladá z piatich rovnoramenných trojuholníkov, napr. ABX, BCX, CDX. Aký je uhol pri vrchole X? To je jednoduché. Je to predsa 360° : 5 = 72°. Uhol AXB je stredový uhol kružnice opísanej päťuholníku. Už Euklides vie, že obvodový uhol ADB je polovica stredového uhla AXB, t. j. 36°. Zároveň obvodovými uhlami sú všetky uhly, ktoré vzniknú tak, že každý jeden bod na kružnici spojíte s A aj B. Takže 36° má aj uhol AEB, aj uhol ACB. Je zrejmé, že tieto stredové a obvodové uhly môžeme napísať pre každú stranu päťuholníka, potom aj uhol EDA má 36°, taktiež aj uhol BDC má 36°.

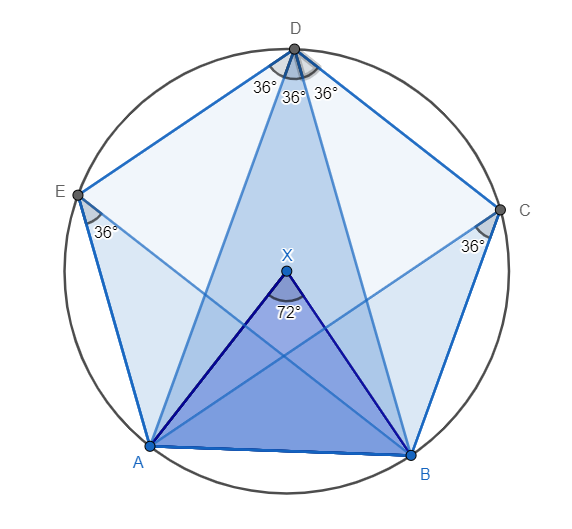
Pozrime sa na druhý obrázok. Vzniknú dva trojuholníky ABY a BDY. Ten BDY má pri vrchole B a D uhol 36°. Tretí uhol dopočítame ako 180° - 36° -36° = 108°. Trojuholník má zasa uhly pri vrchole A 72° a pri vrchole B 36°. Tretí uhol pri vrchole Y možno dopočítať ako 180° - 108° = 72° alebo 180° - 72° - 36° = 72°. Vidíme, že trojuholníky ABY a ABD majú rovnaké uhly pri všetkých svojich vrcholoch, to znamená, že sú podobné. Ak sú podobné, tak potom majú aj rovnaké pomery strán. Môžem zapísať:
DA/AB = BY/YA
Musíme si uvedomiť, že dĺžky úsečiek AB, BY, YD sú rovnako dlhé, lebo ide o strany rovnoramenných trojuholníkov. Potom viem napísať:
DA/YD = YD/YA

Takže mám rovnicu: pomer celej k dlhšej úsečke = pomer dlhšej ku kratšej úsečke. Je to presne definícia zlatého rezu. Čiže bod Y rozdeľuje úsečku v pomere zlatého rezu.